SKループが「悪魔的」戦略に分類され、「極限」戦略ではない理由は、これが非常に際立ったパターンだからです。しかし、この技法はイースターモンスターを解こうとして発見(発明?)されたもので、候補数の多い密集した状態が必要で、これは最も困難なパズルの特徴です。
クレジットとして:オーストラリア・シドニーのpjbまたはPhil氏によるこの解説と、彼のウェブサイトで収集された多くの例に感謝します。このソルバーは、Philのバニラタイプからタイプ Hまでの全てのSKループを見つけますが、まだ「関連ループ」には対応していません。私の実装では「タイプ」を区別せず、検出を一般化しています。SKループは、より大きな何かの一部分のようですが、まだその辺りは探求していません。
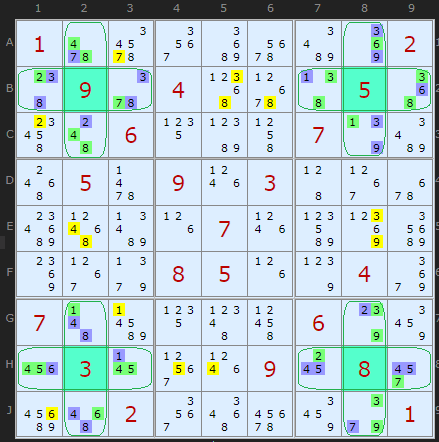
Philと同様に、イースターモンスターから始めましょう。パターンがきれいに広がっており、対称的だからです。SKループは双方向の連続ループで、ループはどの点からでも開始でき、どちらの方向にもリンクを辿ることができます。
まず、4つのボックスに散らばった4つの解けたセルまたは与えられたセルを見つけて、それらが長方形を形成するようにします。Philは与えられたセル(ヒント)と解けたセルを区別しますが、私は区別せず、これによる偽陽性は見つかっていません。
図に示されているのは、そのような4つの数字と、それらを囲む8つの隠れペアを含む2セルペアです。
パターンの定義は次のとおりです:
- ループには2つのバンドと2つのスタックの4つのボックス、および8つのリンクが必要で、各ボックスに1つのリンク、各行に1つのリンク、各列に1つのリンクがあります。
- 各ボックスで、行セルと列セルの交点にあるセルは与えられた数字です。
- ループには単一、二重、または三重のリンクを含めることができますが、リンクの合計は16以下でなければなりません。
- ボックス内の行または列に関与する2つのセルのうち、1つは解けていても構いませんが、与えられたセルであってはいけません。
8つのセルペアがあるので、これらすべてのセルを埋めるには16の数字が必要です。ソルバーは候補を緑と青でハイライトします。これらは代替解です。16個のセル全てに緑の数字または青の数字のいずれかが入り、各ペアで正確に1つの緑と1つの青が入ります(曖昧に聞こえますが、ここの最初の例は後者の例で、コメントでRobertが指摘したとおりです)。
パターン定義ではリンクの合計は16以下が必要です。何を数えているかを見るために、ループの正式な定義を以下に示します:
(27=38)B13- (38=16)B79- (16=39)AC8- (39=27)GJ8- (27=45)H79- (45=16)H13- (16=48)GJ2- (48=27)AC2-
ソルバーは常に左上の与えられたセルから開始し、時計回りにループするので、ペアB13から始まります(Philの文書では異なる場所から始まります)。B13は隠れペア{3,8}でB79と強くリンクしています。すべてのリンクを見て、各ペアの候補を数えると:
これらの数字の合計は16になります。
これら16のセルの内容をロックセットとして特定したので、整列の単位に沿って除去できます。つまり、B13が青の{3,8}を含み、B79が緑の{3,8}を含み、解はどちらか一方なので、B5とB6から3と8を除去できます。
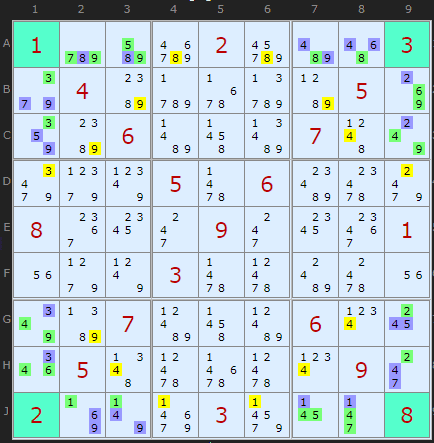
このSKループは、クラシックな全体的なダブルではなく、トリプルとシングルリンクを交互に使用します。これによりタイプは3-1-3-1-3-1-3-1-になりますが、これらの数字の合計は依然として16です。
図のリンクをいくつか辿ってみて、ループの定義と比較してください:
(579=8)A23- (8=469)A78- (469=2)BC9- (2=457)GH9- (457=1)J78- (1=469)J23- (469=3)GH1- (3=579)BC1-
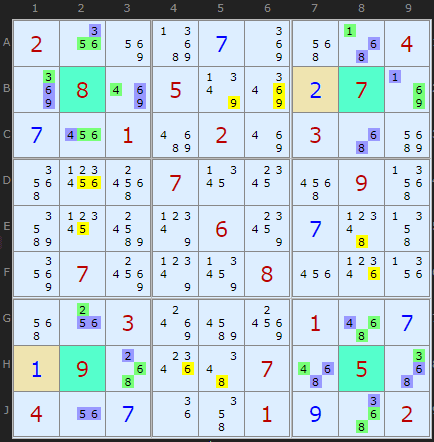
最後に、SKループ定義の4番目の要素、ペアの2つのセルのうち1つが解けたセルである場合を考えることができます。Philは、これは与えられたセルではあり得ないと述べていますが、私はまだ反例を探しており、ソルバーは区別しません。
このループのタイプ2-2-1-2-2-2-1-2-は、現在14にしか合計されません。これは、2つのセル(ベージュ色)が使用されたため正しいです。
(34=69)B13- (69=1)B79- (1=68)AC8- (68=34)GJ8- (34=68)H79- (68=2)H13- (2=56)GJ2- (56=34)AC2-
例
Philが彼のヘルプページで提供している優秀なリストを重複させることはしません。
この記事はSudokuWiki.orgから翻訳されました。

